已知集合A={1,3,4,5},集合B={x∈Z|x2﹣4x﹣5<0},则A∩B的子集个数为( )
A.2 B.4 C.8 D.16
知识点:3.集合的基本运算
C
【考点】1E:交集及其运算.
【分析】求出集合B,根据集合的基本运算进行求解即可.
【解答】解:B={x∈Z|x2﹣4x﹣5<0}=B={x∈Z|﹣1<x<5}={0,1,2,3,4},
则A∩B={1,3,4},
故A∩B的子集个数为23=8个,
故选:C
已知复数Z的共轭复数
 =
= ,则复数Z的虚部是( )
,则复数Z的虚部是( )
A.
 B.
B.
 i C.﹣
i C.﹣
 D.﹣
D.﹣
 i
i
知识点:1.数系的扩充和复数的概念
A
【考点】A5:复数代数形式的乘除运算;A2:复数的基本概念.
【分析】利用复数代数形式的乘除运算化简,求得Z后得答案.
【解答】解:由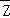
 =
=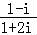 =
=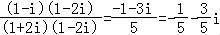 ,
,
得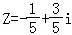 ,
,
∴复数Z的虚部是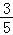
 .
.
故选:A.
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2=( )
A.﹣4 B.﹣6 C.﹣8 D.﹣10
知识点:2.等差数列及其性质
B
【考点】83:等差数列;87:等比数列.
【分析】利用已知条件列出关于a1,d的方程,求出a1,代入通项公式即可求得a2.
【解答】解:∵a4=a1+6,a3=a1+4,a1,a3,a4成等比数列,
∴a32=a1•a4,
即(a1+4)2=a1×(a1+6),
解得a1=﹣8,
∴a2=a1+2=﹣6.
故选B.
设f(x)= ,则
,则 f(x)dx的值为( )
f(x)dx的值为( )
A. +
+
 B.
B. +3 C.
+3 C. +
+
 D.
D. +3
+3
知识点:6.微积分的基本定理
A
【考点】67:定积分.
【分析】根据定积分性质可得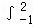 f(x)dx=
f(x)dx=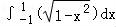 +
+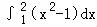 ,然后根据定积分可得.
,然后根据定积分可得.
【解答】解:根据定积分性质可得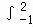 f(x)dx=
f(x)dx= +
+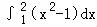 ,
,
根据定积分的几何意义, 是以原点为圆心,以1为半径圆面积的
是以原点为圆心,以1为半径圆面积的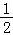
 ,
,
 =
=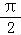
 ,
,
∴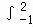 f(x)dx=
f(x)dx=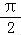 +(
+(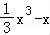 )
)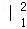 ,
,
=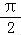 +
+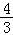
 ,
,
故答案选:A.
执行右面的程序框图,如果输入的N=10,那么输出的S=( )

A. B.
B.
C. D.
D.
知识点:1.算法与程序框图
B
【考点】EF:程序框图.
【分析】从赋值框给出的两个变量的值开始,逐渐分析写出程序运行的每一步,便可得到程序框图表示的算法的功能.
【解答】解:框图首先给累加变量S和循环变量i赋值,
S=0+1=1,k=1+1=2;
判断k>10不成立,执行S=1+ ,k=2+1=3;
,k=2+1=3;
判断k>10不成立,执行S=1+ +
+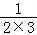 ,k=3+1=4;
,k=3+1=4;
判断k>10不成立,执行S=1+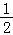 +
+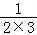 +
+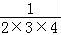 ,k=4+1=5;
,k=4+1=5;
…
判断i>10不成立,执行S=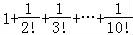 ,k=10+1=11;
,k=10+1=11;
判断i>10成立,输出S=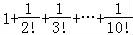 .
.
算法结束.
故选B.
如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为( )

A.
 B.
B.
 C.
C.
 D.2
D.2
知识点:2.空间几何体的三视图和直观图
A
【考点】L!:由三视图求面积、体积.
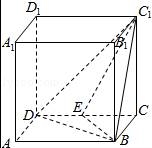
【分析】由四面体的三视图得该四面体为棱长为2的正方体ABCD﹣A1B1C1D1中的三棱锥C1﹣BDE,其中E是CD中点,由此能求出该四面体的体积.
【解答】解:由四面体的三视图得该四面体为棱长为2的正方体ABCD﹣A1B1C1D1中的三棱锥C1﹣BDE,
其中E是CD中点,
△BDE面积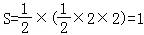 ,三棱锥C1﹣BDE的高h=CC1=2,
,三棱锥C1﹣BDE的高h=CC1=2,
∴该四面体的体积:
V= =
=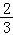
 .
.
故选:A.
已知奇函数f(x) 的定义域为R,若f(x+2)为偶函数,且f(﹣1)=﹣1,则f=( )
A.﹣2 B.﹣1 C.0 D.1
知识点:5.奇偶性与周期性
D
【考点】3L:函数奇偶性的性质.
【分析】根据函数奇偶性的性质,推断出函数的周期是8,利用函数奇偶性和周期性进行转化求解即可.
【解答】解:∵奇函数f(x) 的定义域为R,若f(x+2)为偶函数,
∴f(0)=0,且f(﹣x+2)=f(x+2)=﹣f(x﹣2),
则f(x+4)=﹣f(x),则f(x+8)=﹣f(x+4)=f(x),
则函数f(x)的周期是8,且函数关于x=2对称,
则f=f(1)=﹣f(﹣1)=﹣(﹣1)=1,
f=f(0)=0,
则f=0+1=1,
故选:D
某班班会准备从含甲、乙的7人中选取4人发言,要求甲、乙两人至少有一人参加,且若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
A.720种 B.520种 C.600种 D.360种
知识点:2.排列与组合
C
【考点】D8:排列、组合的实际应用.
【分析】分两类:第一类,甲、乙两人只有一人参加,第二类:甲、乙同时参加,利用加法原理即可得出结论.
【解答】解:分两类:第一类,甲、乙两人只有一人参加,则不同的发言顺序有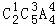 种;
种;
第二类:甲、乙同时参加,则不同的发言顺序有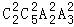 种.
种.
共有: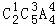 +
+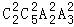 =600(种).
=600(种).
故选:C.
已知抛物线y2=2px(p>0)的焦点为双曲线 ﹣
﹣ =1(a>0,b>0)的右焦点,且其准线被该双曲线截得的弦长是
=1(a>0,b>0)的右焦点,且其准线被该双曲线截得的弦长是 b,则该双曲线的离心率为( )
b,则该双曲线的离心率为( )
A.
 B.
B.
 C.
C.
 D.
D.

知识点:3.抛物线
D
【考点】KC:双曲线的简单性质.
【分析】由题意可知:抛物线的焦点F(c,0),准线x=﹣c,将x=﹣c代入双曲线方程,解得:y=±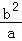 ,即可求得
,即可求得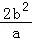 =
=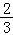
 b,a=3b,利用双曲线的离心率公式,即可求得双曲线的离心率.
b,a=3b,利用双曲线的离心率公式,即可求得双曲线的离心率.
【解答】解:由题意可知:抛物线的焦点F(c,0),准线x=﹣c,
将x=﹣c代入双曲线方程,解得:y=±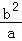 ,
,
则准线被该双曲线截得的弦长为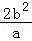 ,
,
∴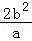 =
=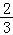
 b,a=3b,
b,a=3b,
双曲线的离心率e=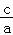
 =
=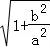 =
=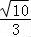 ,
,
则双曲线的离心率e=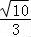 ,
,
故选D.
已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间上单调递减 B.在区间上单调递增
C.在区间上单调递减 D.在区间上单调递增
知识点:7.函数y=Asin(wx+@)+B
B
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.
【分析】根据正弦函数的周期性求得ω,根据函数的图象经过定点求得φ,可得函数f(x)的解析式,再根据y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性得出结论.
【解答】解:∵函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是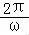
 =π,∴ω=2,
=π,∴ω=2,
将f(x)=sin(2x+φ)的图象向左平移 个单位长度后,可得y=sin(2x+
个单位长度后,可得y=sin(2x+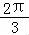
 +φ)的图象,
+φ)的图象,
再根据所的图象过点P( 0,1),∴sin(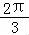 +φ)=1,∴φ=﹣
+φ)=1,∴φ=﹣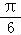 ,故f(x)=sin(2x﹣
,故f(x)=sin(2x﹣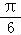 ).
).
在区间上,2x﹣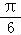 ∈,函数f(x)在区间上单单调递增,
∈,函数f(x)在区间上单单调递增,
故A错误,且B正确.
在区间上,2x﹣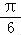 ∈,故函数f(x)在区间上没有单调性,故排除C、D,
∈,故函数f(x)在区间上没有单调性,故排除C、D,
故选:B.
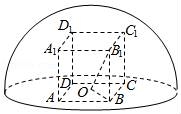
如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为
 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )

A.1 B.
 C.
C.
 D.2
D.2
知识点:3.空间几何体的表面积与体积
D
【考点】LR:球内接多面体.
【分析】设AB=a,BB1=h,求出a2=6﹣2h2,故正四棱柱的体积是V=a2h=6h﹣2h3,利用导数,得到该正四棱柱体积的最大值,即可得出结论.
【解答】解:设AB=a,BB1=h,
则OB= a,连接OB1,OB,则OB2+BB12=OB12=3,
a,连接OB1,OB,则OB2+BB12=OB12=3,
∴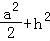 =3,
=3,
∴a2=6﹣2h2,
故正四棱柱的体积是V=a2h=6h﹣2h3,
∴V′=6﹣6h2,
当0<h<1时,V′>0,1<h<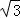
 时,V′<0,
时,V′<0,
∴h=1时,该四棱柱的体积最大,此时AB=2.
故选:D.
已知函数f(x)=sin x﹣1(x<0),g(x)=logax(a>0,且a≠1).若它们的图象上存在关于y轴对称的点至少有3对,则实数a的取值范围是( )
x﹣1(x<0),g(x)=logax(a>0,且a≠1).若它们的图象上存在关于y轴对称的点至少有3对,则实数a的取值范围是( )
A.(0,
 ) B.(
) B.(
 ,1) C.(﹣∞,﹣1) D.(0,
,1) C.(﹣∞,﹣1) D.(0,
 )
)
知识点:7.函数y=Asin(wx+@)+B
A
【考点】H2:正弦函数的图象.
【分析】利用数形结合的思想,做出函数f(x)=sin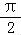
 x﹣1(x<0),关于y轴对称的图象,利用g(x)=logax(a>0,且a≠1)的图象与函数f(x)=sin
x﹣1(x<0),关于y轴对称的图象,利用g(x)=logax(a>0,且a≠1)的图象与函数f(x)=sin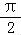
 x﹣1(x>0有至少有3对,可得答案.
x﹣1(x>0有至少有3对,可得答案.
【解答】解:函数f(x)=sin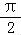 x﹣1(x<0),关于y轴对称的图象如下.
x﹣1(x<0),关于y轴对称的图象如下.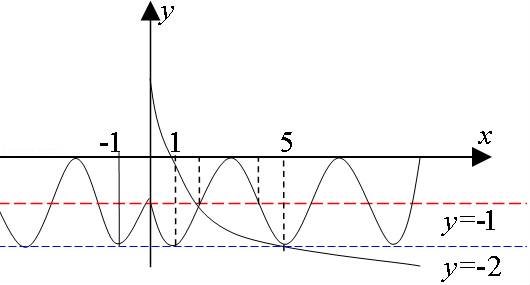
g(x)=logax(a>0,且a≠1)的图象与函数f(x)=sin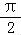 x﹣1(x>0)有至少有3对,
x﹣1(x>0)有至少有3对,
那么:loga5>﹣2,(0<a<1).
可得:a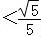 ,
,
∵0<a<1,
∴a∈(0,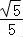 ).
).
故选A.
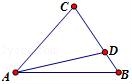
在△ABC中,D为BC上靠近B点的三等分点,连接AD,若 =m
=m +n
+n ,则m+n= .
,则m+n= .
知识点:3.平面向量的基本定理及其坐标表示
1
【考点】9H:平面向量的基本定理及其意义.
【分析】利用向量的三角形法则和向量共线定理即可得出.
【解答】解: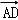
 =
=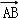
 +
+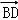
 =
=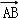
 +
+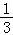

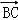
 =
=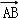
 +
+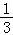
 (
(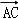
 ﹣
﹣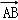
 )=
)=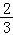

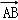
 +
+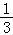

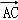
 ,
,
∵
 =m
=m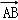
 +n
+n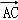
 ,
,
∴m=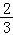
 ,n=
,n=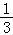
 ,
,
∴m+n=1,
故答案为:1
已知x,y满足约束条件 ,且z=2x+4y的最小值为6,则常数k= .
,且z=2x+4y的最小值为6,则常数k= .
知识点:3.二元一次不等式(组)与简单的线性规划
﹣3
【考点】7C:简单线性规划.
【分析】由约束条件作出可行域,化目标函数为直线方程斜截式,由图得到可行域内的最优解,求出最优解的坐标,代入目标函数后由z的值等于6求得k的值.
【解答】解:由约束条件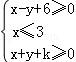 作可行域如图,
作可行域如图,
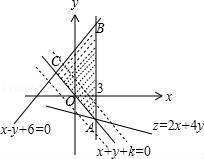
图中以k=0为例,可行域为△ABC及其内部区域,
当k<0,边界AC下移,当k>0时,边界AC上移,均为△ABC及其内部区域.
由z=2x+4y,得直线方程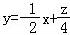 ,
,
由图可知,当直线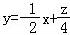 过可行域内的点A时,z最小.
过可行域内的点A时,z最小.
联立 ,得A(3,﹣k﹣3).
,得A(3,﹣k﹣3).
∴zmin=2×3+4(﹣k﹣3)=﹣4k﹣6=6,解得k=﹣3.
故答案为:﹣3.
下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“∃x0∈R,x02﹣x0﹣1>0”的否定是¬P:“∀x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(﹣1<X<0)=
 ﹣p
﹣p
④回归直线一定过样本点的中心(
 ,
,
 ).
).
其中正确的说法有 (请将你认为正确的说法的序号全部填写在横线上)
知识点:4.回归分析的基本思想及其初步应用
②③④
【考点】BS:相关系数.
【分析】①用相关指数R2来刻画回归效果时,R2越大,模型的拟合效果越好;
②根据特称命题的否定的全称命题,写出P的否定¬P即可;
③根据正态分布N(0,1)的性质,由P(X>1)=p求出P(﹣1<X<0)的值;
④回归直线一定过样本点的中心(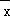
 ,
,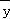
 ).
).
【解答】解:对于①,用相关指数R2来刻画回归效果时,
R2越大,说明模型的拟合效果越好,∴①错误;
对于②,命题P:“∃x0∈R,x02﹣x0﹣1>0”的否定是
¬P:“∀x∈R,x2﹣x﹣1≤0”,②正确;
对于③,根据正态分布N(0,1)的性质可得,
若P(X>1)=p,则P(X<﹣1)=p,
∴P(﹣1<X<1)=1﹣2p,
∴P(﹣1<X<0)=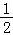
 ﹣p,③正确;
﹣p,③正确;
对于④,回归直线一定过样本点的中心(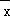
 ,
,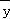
 ),正确;
),正确;
综上,正确的说法是②③④.
故答案为:②③④.
已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn=
 (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
(3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
知识点:6.数列的求和
(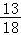 ,+∞)
,+∞)
【考点】8H:数列递推式.
【分析】由{bn}的前n项和为Sn=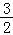
 (3n﹣1)求得bn,进一步得到an,把an,bn代入λan>bn+36(n﹣3)+3λ,分离λ,然后求出关于n的函数的最大值得答案.
(3n﹣1)求得bn,进一步得到an,把an,bn代入λan>bn+36(n﹣3)+3λ,分离λ,然后求出关于n的函数的最大值得答案.
【解答】解:由Sn=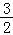
 (3n﹣1),得
(3n﹣1),得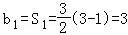 ,
,
当n≥2时, ,
,
当n=1时,上式成立,∴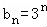 .
.
代入an=2bn+3,得 ,
,
代入λan>bn+36(n﹣3)+3λ,得λ(an﹣3)>bn+36(n﹣3),
即2λ•3n>3n+36(n﹣3),
则λ>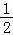
 +
+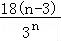 .
.
由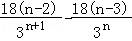 =
=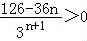 ,得n≤3.
,得n≤3.
∴n=4时,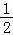
 +
+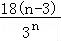 有最大值为
有最大值为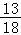
 .
.
故答案为:(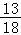 ,+∞).
,+∞).
设△ABC的内角A、B、C的对边长分别为a、b、c.设S为△ABC的面积,满足S= (a2+c2﹣b2).
(a2+c2﹣b2).
(Ⅰ)求B;
(Ⅱ)若b= ,求(
,求( ﹣1)a+2c的最大值.
﹣1)a+2c的最大值.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】HT:三角形中的几何计算.
【分析】(Ⅰ)利用三角形的面积公式表示出S,利用余弦定理表示出cosB,代入已知等式求出tanB的值,即可求出B,
(Ⅱ)先求出A的范围,再根据正弦定理表示出a,c,根据两角和差的正弦公式,正弦函数的图象和性质即可求出最大值
【解答】解:(Ⅰ)∵S=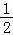
 acsinB,cosB=
acsinB,cosB=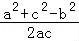 即a2+c2﹣b2=2accosB,
即a2+c2﹣b2=2accosB,
∴S=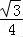 (a2+c2﹣b2)变形得:
(a2+c2﹣b2)变形得: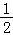 acsinB=
acsinB=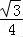 ×2accosB,
×2accosB,
整理得:tanB=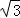
 ,
,
又0<B<π,
∴B=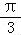
 ,
,
(Ⅱ)∵A+B+C=π,
∴0<A<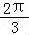
 ,
,
由正弦定理知a= =
=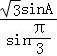 =2sinA,
=2sinA,
c=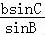 =2sin(
=2sin(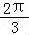 ﹣A),
﹣A),
∴(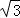 ﹣1)a+2c=2(
﹣1)a+2c=2(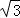
 ﹣1)sinA+4sin(
﹣1)sinA+4sin(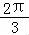 ﹣A)=2
﹣A)=2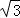 sinA+2
sinA+2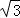 cosA=2
cosA=2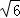
 sin(A+
sin(A+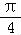 )≤2
)≤2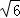
 ,
,
当且仅当A=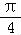
 时取最大值,
时取最大值,
故(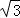 ﹣1)a+2c的最大值为2
﹣1)a+2c的最大值为2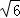
 .
.
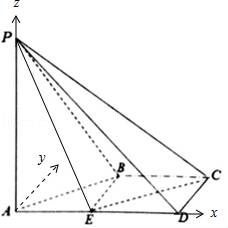
如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=
 AD,E为AD的中点,异面直线AP与CD所成的角为90°.
AD,E为AD的中点,异面直线AP与CD所成的角为90°.
(Ⅰ)证明:△PBE是直角三角形;
(Ⅱ)若二面角P﹣CD﹣A的大小为45°,求二面角A﹣PE﹣C的余弦值.

知识点:10.空间角与距离
【考点】MT:二面角的平面角及求法;LZ:平面与平面垂直的性质.
【分析】(Ⅰ)由已知证明PA⊥平面ABCD,得PA⊥BE.再由已知证明四边形BCDE为平行四边形,得BE∥CD.结合CD⊥AD,得BE⊥AD.再由线面垂直的判定得BE⊥平面PAD,进一步得到BE⊥PE,得到△PBE是直角三角形;
(Ⅱ)由(Ⅰ)知,CD⊥平面PAD,则∠PDA为二面角P﹣CD﹣A的平面角为45°,设BC=1,得AD=PA=2.在平面ABCD中,过A作Ay⊥AD.以A为原点,分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系.求得E,P,C的坐标,求出平面PEC与平面PAE的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PE﹣C的余弦值.
【解答】(Ⅰ)证明:如图,
∵AD∥BC,AD=2BC,∴四边形ABCD为梯形,则AB与DC相交.
∵∠PAB=90°,∴PA⊥AB,
又异面直线AP与CD所成的角为90°,∴PA⊥CD.
∴PA⊥平面ABCD,则PA⊥BE.
∵AD∥BC,BC=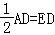
 ,
,
∴四边形BCDE为平行四边形,则BE∥CD.
∵∠ADC=90°,∴CD⊥AD,
∴BE⊥AD.
由BE⊥PA,BE⊥AD,PA∩AD=A,得BE⊥平面PAD,
∴BE⊥PE,则△PBE是直角三角形;
(Ⅱ)解:由(Ⅰ)知,CD⊥平面PAD,则∠PDA为二面角P﹣CD﹣A的平面角为45°,
设BC=1,则AD=PA=2.
在平面ABCD中,过A作Ay⊥AD.
以A为原点,分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系.
则E(1,0,0),P(0,0,2),C(2,1,0).
 .
.
设平面PEC的一个法向量为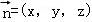 .
.
由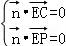 ,得
,得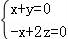 ,取z=1,得
,取z=1,得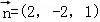 .
.
由图可知,平面PAE的一个法向量为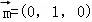 .
.
∴cos<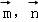 >=
>=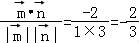 .
.
∴二面角A﹣PE﹣C的余弦值为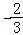 .
.
已知圆E:(x+
 )2+y2=16,点F(
)2+y2=16,点F(
 ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹Γ的方程;
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹Γ的方程;
(Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
 =
=
 ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
知识点:4.直线与圆的位置关系
【考点】JE:直线和圆的方程的应用.
【分析】(I)利用椭圆的定义即可得出E的轨迹方程;
(II)讨论直线l的斜率,联立方程组,利用根与系数的关系得出M点坐标,根据平行四边形对角线互相平分得出R点坐标,代入椭圆方程化简即可得出直线l的斜率k.
【解答】解:(I))∵|QE|+|QF|=|EQ|+|QP|=4,且|EF|=2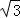
 <4,
<4,
∴点Q的轨迹是以E,F为焦点的椭圆,
设椭圆方程为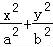 =1,则2a=4,c=
=1,则2a=4,c=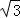
 ,∴a=2,b=
,∴a=2,b=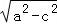 =1.
=1.
所以点E的轨迹方程为: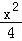 +y2=1.
+y2=1.
(II)(1)当直线l与x轴垂直时,直线l的方程为x=1,显然四边形OARB是平行四边形;
(2)当直线l与x轴不垂直时,设直线l:y=kx+m,显然k≠0,m≠0,
设A(x1,y1),B(x2,y2),M(xM,yM).
联立方程组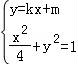 ,得(4k2+1)x2+8kmx+4m2﹣4=0,
,得(4k2+1)x2+8kmx+4m2﹣4=0,
∴x1+x2=﹣
 ,
,
∵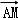
 =
=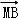
 ,即M是AB的中点,
,即M是AB的中点,
∴xM=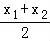 =﹣
=﹣ ,yM=kxM+m=
,yM=kxM+m=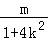
 ,
,
若四边形OARB是平行四边形,当且仅当AB,OR互相平分,
∴R(﹣ ,
,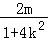 ),
),
代入椭圆方程得: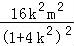 +
+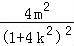 =1,即16k2m2+4m2=16k4+8k2+1,
=1,即16k2m2+4m2=16k4+8k2+1,
又直线l:y=kx+m经过点(1,1),∴m=1﹣k,
∴16k2(1﹣k)2+4(1﹣k)2=16k4+8k2+1,
∴32k3﹣12k2+8k﹣3=0,即(4k2+1)(8k﹣3)=0.
∴k=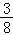
 ,m=
,m=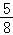
 ,
,
∴直线l的方程为y=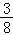
 x+
x+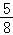
 时,四边形OARB是平行四边形,
时,四边形OARB是平行四边形,
综上,直线l的方程为x=1或y=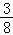
 x+
x+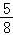
 .
.
已知函数f(x)=ax2﹣(2a﹣1)x﹣lnx(a为常数,a≠0).
(Ⅰ)当a<0时,求函数f(x)在区间上的最大值;
(Ⅱ)记函数f(x)图象为曲线C,设点A(x1,y1),B(x2,y2)是曲线C上不同的两点,点M为线段AB的中点,过点M作x轴的垂线交曲线C于点N.判断曲线C在点N处的切线是否平行于直线AB?并说明理由.
知识点:3.导数在研究函数中的应用
【考点】6E:利用导数求闭区间上函数的最值;6H:利用导数研究曲线上某点切线方程.
【分析】(Ⅰ)求出函数f(x)的导数,通过讨论a的范围,求出函数f(x)的单调区间,从而求出f(x)的最大值即可;
(Ⅱ)设出M的坐标,分别求出直线AB的斜率k1,C在点N处的切线斜率k2,由k1=k2,得到即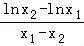 =﹣
=﹣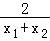 ,得出矛盾.
,得出矛盾.
【解答】解:(Ⅰ)f′(x)=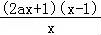 ,
,
当a<0时,由f′(x)=0,得x1=﹣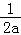
 ,x2=1,又x∈,则有如下分类:
,x2=1,又x∈,则有如下分类:
①当﹣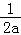
 ≥2,即﹣
≥2,即﹣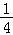
 ≤a<0时,f(x)在上是增函数,
≤a<0时,f(x)在上是增函数,
所以f(x)max=f(2)=2﹣ln2.
②当1<﹣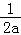
 <2,即﹣
<2,即﹣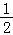
 <a<﹣
<a<﹣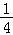
 时,f(x)在上是减函数,
时,f(x)在上是减函数,
所以f(x)max=f(﹣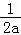
 )=1﹣
)=1﹣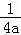
 +ln(﹣2a).
+ln(﹣2a).
③当﹣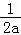
 ≤1,即a≤﹣
≤1,即a≤﹣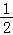
 时,f(x)在上是减函数,
时,f(x)在上是减函数,
所以f(x)max=f(1)=1﹣a.
综上,函数f(x)在上的最大值为:
f(x)max=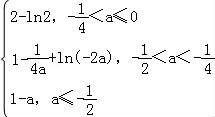 ;
;
(Ⅱ)设M(x0,y0),则点N的横坐标为x0=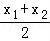
 ,
,
直线AB的斜率k1= =
=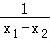
=a(x1+x2)+(1﹣2a)+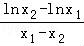 ,
,
C在点N处的切线斜率
k2=f′(x0)=a(x1+x2)+(1﹣2a)﹣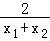 ,
,
假设曲线C在点N处的切线平行于直线AB,则k1=k2,
即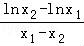 =﹣
=﹣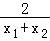 ,所以ln
,所以ln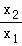
 =
=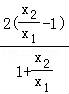 ,
,
不妨设x1<x2,ln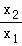 =t>1,则lnt=
=t>1,则lnt=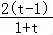 ,
,
令g(t)=lnt﹣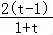 ,(t>1),g′(t)=
,(t>1),g′(t)= >0,
>0,
所以g(t)在(1,+∞)上是增函数,又g(1)=0,
所以g(t)>0,即lnt=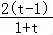
 不成立,
不成立,
所以曲线C在点N处的切线不平行于直线AB.
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为
 .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
知识点:2.坐标系与参数方程
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.
【分析】(Ⅰ)曲线C的极坐标方程化为ρ2﹣4ρcosθ+3ρ2sin2θ=0,由此能求出曲线C的直角坐标方程;由直线l过点M(1,0),倾斜角为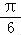
 ,能求出直线l的参数方程.
,能求出直线l的参数方程.
(Ⅱ)由曲线C经过伸缩变换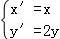 后得到曲线C′,求出曲线C′为:(x﹣2)2+y2=4,把直线l的参数方程代入曲线C′,得:
后得到曲线C′,求出曲线C′为:(x﹣2)2+y2=4,把直线l的参数方程代入曲线C′,得: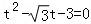 ,设A,B对应的参数分别为t1,t2,则t1+t2=
,设A,B对应的参数分别为t1,t2,则t1+t2=
 ,t1t2=﹣3,由此能求出|MA|+|MB|.
,t1t2=﹣3,由此能求出|MA|+|MB|.
【解答】解:(Ⅰ)∵曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,∴ρ2﹣4ρcosθ+3ρ2sin2θ=0,
∴曲线C的直角坐标方程为x2+y2﹣4x+3y2=0,整理,得(x﹣2)2+4y2=4,
∵直线l过点M(1,0),倾斜角为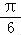
 ,
,
∴直线l的参数方程为 ,即
,即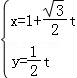 ,(t是参数).
,(t是参数).
(Ⅱ)∵曲线C经过伸缩变换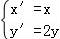 后得到曲线C′,
后得到曲线C′,
∴曲线C′为:(x﹣2)2+y2=4,
把直线l的参数方程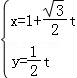 ,(t是参数)代入曲线C′:(x﹣2)2+y2=4,得:
,(t是参数)代入曲线C′:(x﹣2)2+y2=4,得:
 ,
,
设A,B对应的参数分别为t1,t2,则t1+t2=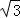
 ,t1t2=﹣3,
,t1t2=﹣3,
∴|MA|+|MB|=|t1|+|t2|=|t1﹣t2|=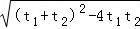 =
=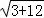 =
=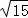 .
.
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
知识点:3.不等式选讲
【考点】R5:绝对值不等式的解法;R4:绝对值三角不等式.
【分析】(Ⅰ)通过讨论x的范围,得到关于x的不等式组,解出即可;(Ⅱ)求出f(x)的最小值,解关于m的不等式,解出即可.
【解答】解:(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化为①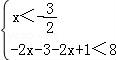 或②
或②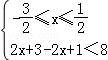 或③
或③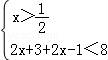 ,…
,…
解①得﹣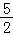
 <x<﹣
<x<﹣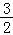
 ,解②得﹣
,解②得﹣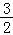
 ≤x≤
≤x≤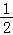
 ,解③得
,解③得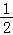
 <x<
<x<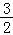
 ,
,
综合得:﹣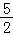
 <x<
<x<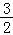
 ,即原不等式的解集为{x|﹣
,即原不等式的解集为{x|﹣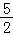
 <x<
<x<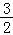
 }.…
}.…
(Ⅱ)因为∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
当且仅当﹣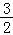
 ≤x≤
≤x≤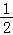
 时,等号成立,即f(x)min=4,…
时,等号成立,即f(x)min=4,…
又不等式f(x)≤|3m+1|有解,则|3m+1|≥4,解得:m≤﹣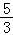
 或m≥1.…
或m≥1.…