已知全集U=R,A={y|y=2x+1},B={x|lnx≥0},则A∩B=( )
A.{x|x≥1} B.{x|x>1} C.{x|0<x<1} D.∅
知识点:3.集合的基本运算
B
【考点】交集及其运算.
【专题】计算题;集合思想;定义法;集合.
【分析】求解函数的值域化简A,求解对数不等式化简B,然后取交集得答案.
【解答】解:∵A={y|y=2x+1}=(1,+∞),B={x|lnx≥0}=(1,+∞),
∴A∩B=(1,+∞).
故选:B.
【点评】本题考查交集及其运算,考查了函数值域的求法,训练了对数不等式的解法,是基础题.
定义在R的奇函数f(x),当x<0时,f(x)=﹣x2+x,则f(2)等于( )
A.4 B.6 C.﹣4 D.﹣6
知识点:5.奇偶性与周期性
B
【考点】函数奇偶性的性质.
【专题】计算题;方程思想;转化法;函数的性质及应用.
【分析】根据函数奇偶性的性质进行转化求解即可.
【解答】解:∵定义在R的奇函数f(x),当x<0时,f(x)=﹣x2+x,
∴f(2)=﹣f(﹣2)=﹣[﹣(﹣2)2﹣2]=6,
故选:B
【点评】本题主要考查函数值的计算,利用函数奇偶性的性质进行转化是解决本题的关键.
已知向量 =(1,2),2
=(1,2),2 +
+ =(3,2),则( )
=(3,2),则( )
A. =(1,﹣2) B.
=(1,﹣2) B. =(1,2) C.
=(1,2) C. =(5,6) D.
=(5,6) D. =(2,0)
=(2,0)
知识点:3.平面向量的基本定理及其坐标表示
A
【考点】平面向量的坐标运算.
【专题】平面向量及应用.
【分析】设出 ,利用向量的坐标运算求解即可.
,利用向量的坐标运算求解即可.
【解答】解:设 =(x,y),
=(x,y),
向量 =(1,2),2
=(1,2),2 +
+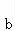 =(3,2),
=(3,2),
可得(2+x,4+y)=(3,2),解得x=1,y=﹣2.
∴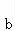 =(1,﹣2).
=(1,﹣2).
故选:A.
【点评】本题考查向量的坐标运算,基本知识的考查.
已知函数f(x)是定义在区间[0,+∞)上的增函数,则满足f(2x﹣1)<f( )的x的取值范围是( )
)的x的取值范围是( )
A.( ,
, ) B.[
) B.[ ,
, ) C.(
) C.( ,
, ) D.[
) D.[ ,
, )
)
知识点:3.单调性与最大(小)值
D
【考点】函数单调性的性质.
【专题】函数的性质及应用.
【分析】由函数的单调性的性质可得 0≤2x﹣1<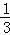 ,由此求得x的取值范围.
,由此求得x的取值范围.
【解答】解:∵函数f(x)是定义在区间[0,+∞)上的增函数,则满足f(2x﹣1)<f(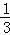 ),
),
∴0≤2x﹣1<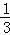 ,解得
,解得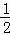 ≤x<
≤x<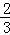 ,
,
故选D.
【点评】本题主要考查函数的单调性的性质,属于基础题.
下列函数中,既在定义域上是增函数且图象又关于原点对称的是( )
A.y=﹣ B.y=lg(
B.y=lg( ﹣1) C.y=2x D.y=2x+2﹣x
﹣1) C.y=2x D.y=2x+2﹣x
知识点:15.函数的图像
C
【考点】函数的图象.
【专题】转化思想;综合法;函数的性质及应用.
【分析】逐一判断各个函数在它的定义域上的单调性以及奇偶性,从而得出结论.
【解答】解:由于y=﹣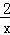 在定义域{x|x≠0}上没有单调性,故排除A;
在定义域{x|x≠0}上没有单调性,故排除A;
由于y=lg( ﹣1)的定义域不关于原点对称,故它不是奇函数,故它的图象一定不关于原点对称,故排除B;
﹣1)的定义域不关于原点对称,故它不是奇函数,故它的图象一定不关于原点对称,故排除B;
由于y=2x在定义域R上是单调递增函数,且是奇函数,故它的图象关于原点对称,故满足条件;
由于 y=2x+2﹣x是偶函数,它的图象关于y轴对称,故不满足条件,
故选:C.
【点评】本题主要考查函数的单调性和奇偶性的判断,函数的图象特征,属于中档题.
函数f(x)=x5+x﹣3的零点所在的区间是( )
A.[0,1] B.[1,2] C.[2,3] D.[3,4]
知识点:13.函数与方程
B
【考点】函数零点的判定定理.
【专题】函数的性质及应用.
【分析】利用函数的单调性和函数零点的判定定理即可得出.
【解答】解:由函数f(x)=x5+x﹣3可知函数f(x)在R上单调递增,又f(1)=1+1﹣3=﹣1<0,f(2)=25+2﹣3>0,
∴f(1)f(2)<0,
因此函数f(x)在(1,2)上存在唯一零点.
故选B.
【点评】本题考查了函数的单调性和函数零点的判定定理,属于基础题.
若α,β都是锐角,且 ,则cosβ=( )
,则cosβ=( )
A. B.
B. C.
C. 或
或 D.
D. 或
或
知识点:4.和角公式与倍(半)角公式
A
【考点】两角和与差的余弦函数.
【专题】转化思想;综合法;三角函数的求值.
【分析】由条件利用同角三角函数的基本关系,两角差的三角公式,求得cosβ=cos[α﹣(α﹣β)]的值.
【解答】解:∵α,β都是锐角,且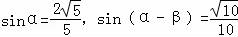 ,
,
∴cosα= =
=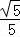 ,cos(α﹣β)=
,cos(α﹣β)= =
=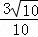 ,
,
则cosβ=cos[α﹣(α﹣β)]=cosαcos(α﹣β)+sinαsin(α﹣β)=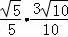 +
+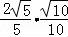
=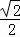 ,
,
故选:A.
【点评】本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.
函数f(x)=sin(2x+φ)|φ|< )的图象向左平移
)的图象向左平移 个单位后关于原点对称,则φ等于( )
个单位后关于原点对称,则φ等于( )
A. B.﹣
B.﹣ C.
C. D.
D.
知识点:7.函数y=Asin(wx+@)+B
D
【考点】函数y=Asin(ωx+φ)的图象变换.
【专题】三角函数的图像与性质.
【分析】由条件根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性可得 +φ=kπ,k∈z,由此根据|φ|<
+φ=kπ,k∈z,由此根据|φ|<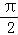 求得φ的值.
求得φ的值.
【解答】解:函数f(x)=sin(2x+φ)φ|<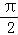 )的图象向左平移
)的图象向左平移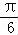 个单位后,得到函数y=sin[2(x+
个单位后,得到函数y=sin[2(x+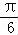 )+φ]=sin(2x+
)+φ]=sin(2x+ +φ)的图象,
+φ)的图象,
再根据所得图象关于原点对称,可得 +φ=kπ,k∈z,∴φ=﹣
+φ=kπ,k∈z,∴φ=﹣ ,
,
故选:D.
【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.
函数y=ln(﹣x2﹣2x+8)的单调递减区间是( )
A.(﹣∞,﹣1) B.(﹣1,2) C.(﹣4,﹣1) D.(﹣1,+∞)
知识点:3.导数在研究函数中的应用
B
【考点】对数函数的图象与性质.
【专题】函数思想;综合法;函数的性质及应用.
【分析】根据对数函数的性质求出x的范围,令t(x)=﹣x2﹣2x+8,根据二次函数的性质求出t(x)的递减区间,从而结合复合函数的单调性求出函数y=ln(﹣x2﹣2x+8)的单调递减区间即可.
【解答】解:由题意得:﹣x2﹣2x+8>0,解得:﹣4<x<2,
∴函数的定义域是(﹣4,2),
令t(x)=﹣x2﹣2x+8,对称轴x=﹣1,
∴t(x)在(﹣1,2)递减,
∴函数y=ln(﹣x2﹣2x+8)的单调递减区间是(﹣1,2),
故选:B.
【点评】本题考查了二次函数、对数函数的性质,考查复合函数的单调性问题,是一道基础题.
已知 =(2,m),
=(2,m), =(﹣1,m),若(2
=(﹣1,m),若(2 ﹣
﹣ )⊥
)⊥ ,则|
,则| |=( )
|=( )
A.2 B.3 C.4 D.5
知识点:4.平面向量的数量积(夹角、模)
B
【考点】向量的模.
【专题】计算题;对应思想;向量法;平面向量及应用.
【分析】化简可得2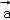 ﹣
﹣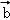 =(5,m),故(5,m)(﹣1,m)=0,从而求得m2=5,从而求|
=(5,m),故(5,m)(﹣1,m)=0,从而求得m2=5,从而求|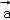 |.
|.
【解答】解:2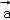 ﹣
﹣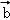 =2(2,m)﹣(﹣1,m)=(5,m),
=2(2,m)﹣(﹣1,m)=(5,m),
∵(2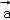 ﹣
﹣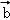 )⊥
)⊥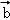 ,
,
∴(5,m)(﹣1,m)=0,
即5﹣m2=0,即m2=5,
故|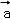 |=
|=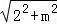 =3;
=3;
故选:B.
【点评】本题考查了平面向量的线性运算及数量积的应用,同时考查了向量的模的求法.
已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,|φ|< )的部分图象如图所示,则φ=( )
)的部分图象如图所示,则φ=( )
A. B.
B. C.
C. D.
D.
知识点:7.函数y=Asin(wx+@)+B
B
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;正弦函数的图象.
【专题】三角函数的图像与性质.
【分析】结合函数的图象,由函数的最值求出A,由周期求出ω,再由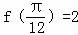 求出φ的值.
求出φ的值.
【解答】解:由图可知A=2, ,故ω=2,
,故ω=2,
又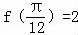 ,
,
所以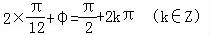 ,
,
故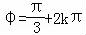 ,
,
又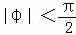 ,
,
所以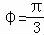 .
.
故选:B.
【点评】本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.
已知函数f(x)= 若函数g(x)=f[f(x)]﹣2的零点个数为( )
若函数g(x)=f[f(x)]﹣2的零点个数为( )
A.3 B.4 C.5 D.6
知识点:13.函数与方程
B
【考点】函数零点的判定定理.
【专题】数形结合;方程思想;转化思想;转化法;函数的性质及应用.
【分析】函数f(x)= ,通过对x分类讨论可得f(x)=
,通过对x分类讨论可得f(x)= .进而解出即可.
.进而解出即可.
【解答】解:∵函数f(x)=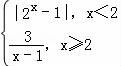 ,
,
∴f(x)= .
.
∴x∈(﹣∞,log23)时,f(f(x))= ∈[0,3],令f(f(x))=2,解得x=log2(1+log23).
∈[0,3],令f(f(x))=2,解得x=log2(1+log23).
同理可得:x∈[log23,2)时,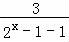 =2,解得x=
=2,解得x=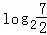 .
.
x∈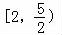 时,
时,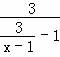 =2,解得x=
=2,解得x=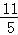 .
.
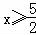 时,
时,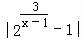 =2,解得x=1+
=2,解得x=1+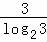 .
.
综上可得:函数g(x)=f[f(x)]﹣2的x零点个数为4.
故选:B.
【点评】本题考查了函数的性质、不等式的解法、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于难题.
若a=0.32,b=log20.3,c=20.3,则a,b,c的大小关系(由小到大是) .
知识点:16函数值的大小比较
b<a<c
【考点】对数值大小的比较.
【专题】计算题.
【分析】由0<a=0.32<1,b=log20.3<log21=0,c=20.3>20=1,能判断a,b,c的大小关系.
【解答】解:∵0<a=0.32<1,
b=log20.3<log21=0,
c=20.3>20=1,
∴b<a<c.
故答案为:b<a<c.
【点评】本题考查a,b,c的大小关系的判断,解题时要认真审题,注意对数函数、指数函数的性质的灵活运用.
化简2sin15°sin75°的值为 .
知识点:4.和角公式与倍(半)角公式
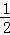
【考点】二倍角的正弦.
【专题】计算题;转化思想;三角函数的求值.
【分析】利用诱导公式,二倍角的正弦函数公式化简所求后,利用特殊角的三角函数值即可得解.
【解答】解:2sin15°sin75°
=2sin15°sin(90°﹣15°)
=2sin15°cos15°
=sin30°
=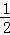 .
.
故答案为: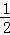 .
.
【点评】本题主要考查了诱导公式,二倍角的正弦函数公式,特殊角的三角函数值在三角函数化简求值中的应用,属于基础题.
若tanα,tanβ是方程x2﹣3 x+4=0的两个根,则tan(α+β)= .
x+4=0的两个根,则tan(α+β)= .
知识点:4.和角公式与倍(半)角公式
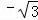
【考点】两角和与差的正切函数.
【专题】计算题;方程思想;数学模型法;三角函数的求值.
【分析】利用一元二次方程的根与系数的关系求出tanα+tanβ=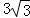 ,tanαtanβ=4,代入两角和的正切得答案.
,tanαtanβ=4,代入两角和的正切得答案.
【解答】解:∵tanα,tanβ是方程x2﹣3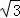 x+4=0的两个根,
x+4=0的两个根,
∴tanα+tanβ=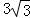 ,tanαtanβ=4,
,tanαtanβ=4,
∴tan(α+β)=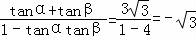 .
.
故答案为: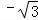 .
.
【点评】本题考查一元二次方程的根与系数的关系的应用,考查了两角和与差的正切,是基础题.
在菱形ABCD中,对角线AC=4,E为CD的中点,则 = .
= .
知识点:4.平面向量的数量积(夹角、模)
12
【考点】平面向量数量积的运算.
【专题】计算题;转化思想;向量法;平面向量及应用.
【分析】设菱形的边长为a,运用向量的加法运算和中点的向量表示,结合向量数量积的性质:向量的平方即为模的平方,运用整体代入,计算即可得到所求值.
【解答】解:设菱形的边长为a,
由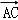 =
=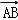 +
+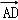 ,可得
,可得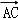 2=
2= 2+
2+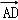 2+2
2+2
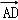 ,
,
即有16=2a2+2
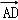 ,
,
即a2+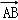
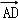 =8,
=8,
则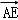
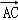 =(
=(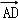 +
+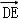 )(
)(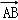 +
+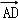 )
)
=(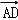 +
+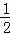
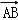 )(
)(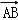 +
+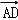 )
)
=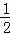
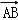 2+
2+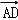 2+
2+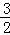
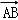
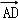
=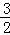 (a2+
(a2+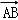
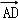 )=
)=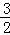 ×8=12.
×8=12.
故答案为:12.
【点评】本题考查向量的运算,主要考查向量的数量积的性质:向量的平方即为模的平方,考查运算能力,属于中档题.
已知坐标平面上的直线与x,y轴分别相交于A(3,0),B(0,3)两点,点C(cosα,sinα),其中 .
.
(1)若 ,求角α的值;
,求角α的值;
(2)若 ,求sin2α的值.
,求sin2α的值.
知识点:4.平面向量的数量积(夹角、模)
【考点】向量的模;平面向量数量积的运算;二倍角的正弦.
【专题】计算题.
【分析】(1)先求出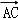 和
和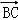 的坐标,根据
的坐标,根据 化简可得cosα=sinα,再由α的范围求出α的值.
化简可得cosα=sinα,再由α的范围求出α的值.
(2)根据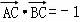 ,化简可得 (cosα+sinα )=
,化简可得 (cosα+sinα )=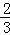 ,再平方可得sin2α 的值.
,再平方可得sin2α 的值.
【解答】解:(1)∵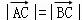 ,
, =(cosα﹣3,sinα ),
=(cosα﹣3,sinα ),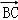 =(cosα,sinα﹣3),
=(cosα,sinα﹣3),
∴(cosα﹣3)2+sin2α=cos2α+(sinα﹣3)2.
化简可得 cosα=sinα.
又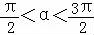 ,∴α=
,∴α=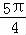 .
.
(2)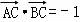 ,则 (cosα﹣3)cosα+sinα (sinα﹣3)=﹣1,
,则 (cosα﹣3)cosα+sinα (sinα﹣3)=﹣1,
化简可得 (cosα+sinα )=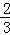 .
.
平方可得 1+sin2α=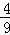 ,∴sin2α=﹣
,∴sin2α=﹣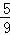 .
.
【点评】本题主要考查两个向量坐标形式的运算,求向量的模的方法,二倍角公式的应用,属于基础题.
已知 (ω>0),记f(x)=
(ω>0),记f(x)= .且f(x)的最小正周期为π.
.且f(x)的最小正周期为π.
(1)求f(x)的最大值及取得最大值时x的集合;
(2)求f(x)在区间 上的取值范围.
上的取值范围.
知识点:4.平面向量的数量积(夹角、模)
【考点】平面向量数量积的运算;三角函数中的恒等变换应用;正弦函数的图象.
【专题】综合题;函数思想;综合法;三角函数的图像与性质.
【分析】(1)由向量数量积的坐标运算结合辅助角公式化简,再由周期求得ω,则函数解析式可求,由此求得f(x)的最大值及取得最大值时x的集合;
(2)由x得范围求得相位的范围,进一步求得f(x)在区间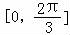 上的取值范围.
上的取值范围.
【解答】解:(1)f(x)=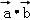 =
=
=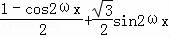 =
=
=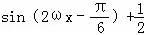 .
.
∵函数f(x)的最小正周期为π,且ω>0,
∴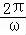 =π,解得ω=1,
=π,解得ω=1,
∴f(x)=sin(2x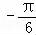 )
)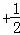 .
.
∴f(x)的最大值为 ,此时
,此时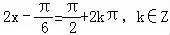 ,即
,即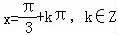 .
.
∴使f(x)取得最大值时x的集合为{x|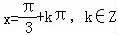 };
};
(2)由(1)得f(x)=sin(2x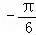 )
)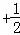 .
.
∵0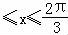 ,
,
∴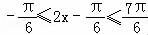 ,
,
∴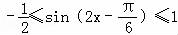 ,
,
因此0≤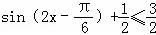 ,
,
即f(x)的取值范围为[0,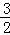 ].
].
【点评】本题考查三角函数中的恒等变换应用,考查了三角函数的图象和性质,训练了平面向量数量积的坐标运算,是中档题.
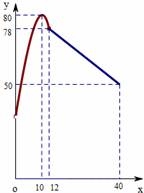
学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

知识点:14.函数的应用问题
【考点】函数解析式的求解及常用方法;函数的最值及其几何意义.
【专题】函数的性质及应用.
【分析】(1)当x∈(0,12]时,设f(x)=a(x﹣10)2+80,把点(12,78)代入能求出解析式;当x∈[12,40]时,设y=kx+b,把点B(12,78)、C(40,50)代入能求出解析式.
(2)由(1)的解析式,结合题设条件,列出不等式组,能求出老师就在什么时段内安排核心内容,能使得学生学习效果最佳
【解答】解:(1)当x∈(0,12]时,
设f(x)=a(x﹣10)2+80…
过点(12,78)代入得,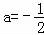
则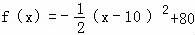 …
…
当x∈[12,40]时,
设y=kx+b,过点B(12,78)、C(40,50)
得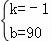 ,即y=﹣x+90…
,即y=﹣x+90…
则的函数关系式为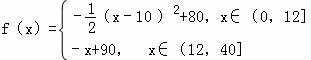 …
…
(2)由题意得,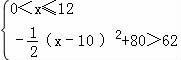 或
或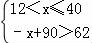 …
…
得4<x≤12或12<x<28,
4<x<28…
则老师就在x∈(4,28)时段内安排核心内容,能使得学生学习效果最佳.…
【点评】本题考查解析式的求法,考查不等式组的解法,解题时要认真审题,注意待定系数法的合理运用.
设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1,x2∈[0, ],都有f(x1+x2)=f(x1)f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)f(x2),且f(1)=a>0.
(1)求f( )及f(
)及f( );
);
(2)证明f(x)是周期函数.
知识点:5.奇偶性与周期性
【考点】函数的周期性;函数奇偶性的性质;函数的图象;抽象函数及其应用.
【专题】计算题.
【分析】(1)已知任意x1,x2∈[0,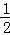 ],都有f(x1+x2)=f(x1)f(x2),令x1=x2=
],都有f(x1+x2)=f(x1)f(x2),令x1=x2=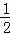 ,求出f(
,求出f(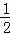 ),根据
),根据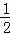 =
=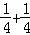 进行求解;
进行求解;
(2)已知f(x)为偶函数,再根据f(x)关于x=1对称,进行证明;
【解答】解;(1)∵f(1)=f(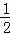 +
+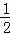 )=f(
)=f(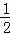 )f(
)f(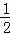 )=f2(
)=f2(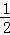 )=a,
)=a,
∴f(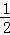 )=±
)=±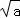
又∵f(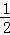 )=f(
)=f(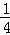 +
+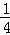 )=f2(
)=f2(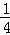 )>0,
)>0,
∴f(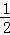 )=
)=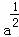 同理可得f(
同理可得f(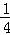 )=
)=
(2)∵f(x)是偶函数,
∴f(﹣x)=f(x)
又∵f(x)关于x=1对称,
∴f(x)=f(2﹣x)
∴f(x)=f(﹣x)=f[2﹣(﹣x)]=f(2+x) (x∈R)
这表明f(x)是R上的周期函数,且2是它的一个周期.
【点评】此题主要考查函数的周期性,此类抽象函数的题,主要利用特殊值法,此题比较简单.
已知函数f(x)=loga (a>0,且a≠1)
(a>0,且a≠1)
(1)判断f(x)的奇偶性并证明;
(2)若对于x∈[2,4],恒有f(x)>loga 成立,求m的取值范围.
成立,求m的取值范围.
知识点:10.对数函数及其性质
【考点】函数恒成立问题;函数奇偶性的判断.
【专题】转化思想;转化法;函数的性质及应用.
【分析】(1)根据函数奇偶性的定义进行判断.
(2)根据对数函数的单调性,将不等式恒成立进行转化,利用参数分离法进行求解即可.
【解答】解:(1)因为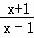 >解得x>1或x<﹣1,
>解得x>1或x<﹣1,
所以函数f(x)的定义域为(﹣∞,﹣1)∪(1,+∞),
函数f(x)为奇函数,证明如下:
由(I)知函数f(x)的定义域关于原点对称,
又因为f(﹣x)=loga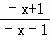 =loga
=loga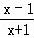 =loga(
=loga(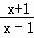 )﹣1=﹣loga
)﹣1=﹣loga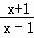 =﹣f(x),
=﹣f(x),
所以函数f(x)为奇函数…
(2)若对于x∈[2,4],f(x)>loga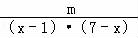 恒成立
恒成立
即loga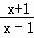 >loga
>loga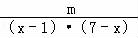 对x∈[2,4]恒成立
对x∈[2,4]恒成立
当a>1时,即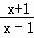 >
>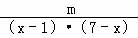 对x∈[2,4]成立.
对x∈[2,4]成立.
则x+1>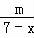 ,即(x+1)(7﹣x)>m成立,
,即(x+1)(7﹣x)>m成立,
设g(x)=(x+1)(7﹣x)=﹣(x﹣3)2+16,
因为x∈[2,4]
所以g(x)∈[15,16],
则0<m<15,
同理当0<a<1时,即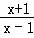 <
<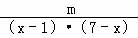 对x∈[2,4]成立.
对x∈[2,4]成立.
则x+1<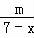 ,即(x+1)(7﹣x)<m成立,
,即(x+1)(7﹣x)<m成立,
设g(x)=(x+1)(7﹣x)=﹣(x﹣3)2+16,
因为x∈[2,4]
所以g(x)∈[15,16],
则m>16,
综上所述:a>1时,0<m<15,
0<a<1时,m>16 ….
【点评】本题主要考查函数奇偶性的判断以及不等式恒成立问题问题,利用对数函数的单调性,利用参数分离法进行求解即可.
函数 .
.
(1)当m= 时,求g(θ)的单调递增区间;
时,求g(θ)的单调递增区间;
(2)若g(θ)+1<0恒成立,求m的取值范围.
知识点:6.三角函数的图像与性质
【考点】三角函数中的恒等变换应用;三角函数的最值.
【专题】计算题;数形结合;数形结合法;函数的性质及应用;三角函数的求值.
【分析】(1)令t=cosθ∈[0,1],可得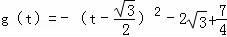 ,可得:g(t)在
,可得:g(t)在 上单调递增,在
上单调递增,在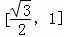 上单调递减,又t=cosθ在
上单调递减,又t=cosθ在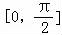 上单调递减,令
上单调递减,令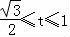 ,即可解得函数f(x)的单调递增区间.
,即可解得函数f(x)的单调递增区间.
(2)由题意可得: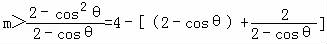 ,由
,由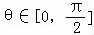 ,可得2﹣cosθ∈[1,2],利用基本不等式即可得解m的取值范围.
,可得2﹣cosθ∈[1,2],利用基本不等式即可得解m的取值范围.
【解答】解:(1)令t=cosθ∈[0,1],可得: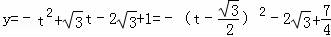 ,
,
记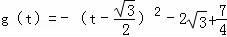 ,可得:g(t)在
,可得:g(t)在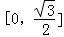 上单调递增,在
上单调递增,在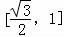 上单调递减.
上单调递减.
又t=cosθ在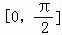 上单调递减.令
上单调递减.令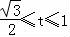 ,解得
,解得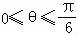 ,
,
故函数f(x)的单调递增区间为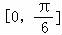 .…
.…
(2)由g(θ)<﹣1得(2﹣cosθ)m>2﹣cos2θ,
即: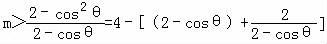 ,
,
∵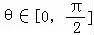 ,
,
∴2﹣cosθ∈[1,2],
∴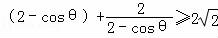 ,等号成立时cosθ=2﹣
,等号成立时cosθ=2﹣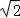 .
.
故:4﹣[(2﹣cosθ)+ ]的最大值是4﹣2
]的最大值是4﹣2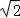 .
.
从而m>4﹣2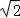 .…
.…
【点评】本题考查二次函数的图象和性质及恒成立问题,考查了基本不等式的应用,考查分类讨论思想,考查学生分析问题解决问题的能力,属于中档题.